HOTJUPITER

Introduction

HOT JUPITER is a pipeline that I developed in IDL between 2007 and 2009 as a graduate student at JHU for the automatic reduction of Hot-Jupiter planet photometry with the IRAC instrument on the Spitzer Space Telescope. Its usage has resulted in three peer-reviewed publications and a thesis. I decided to make the entire pipeline public as an incentive to have all the remaining Cold Spitzer observations of Hot Jupiter secondary eclipses reduced in an expedient manner.

Disclaimer

It is possible, even likely, that there are mistakes, unknown errors and gaping bugs in the programs. Furthermore it is inefficiently written, very longwinded  sometimes made under emotional pain and in stress. It is presented AS IS and I cannot accept any liability whatsoever, if you use the pipeline, publish something and your whole tenure driven career comes to a crashing halt, I warned you.

“We would like to also acknowledge the use of publicly available routines by Eric Agol and Levenberg-Marquardt least squares minimization routine MPFITFUN by Craig Markwardt. P.M. was supported by the Spitzer Science Center grant C4030 to the Space Telescope Science Institute, and the BayArea Environmental Research Institute. This work is based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. This publication also makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the
Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.”

Publications using the pipeline

The thesis can be found here.

• Machalek et al.  2010, Astrophysical Journal Thermal Emission and Tidal Heating of the Heavy and Eccentric Planet XO-3b
• Machalek et al.  2009, Astrophysical Journal Detection of Thermal Emission of XO-2b: Evidence for a Weak Temperature Inversion
• Machalek et al.  2008, Astrophysical Journal Thermal Emission of Exoplanet XO-1b

Programs needed

Download all the programs and files from http://www.pha.jhu.edu/~pmachal2/hotjupiter/

Furthermore you will need all the IDLASTRO routines.

Tutorial

1. Download data from LEOPARD

First download LEOPARD. Use it to search for your favorite target according to program or author.

Then download all the BCD files and have them unzip automatically.

1. Visually inspect images to determine rough centroids

You will need to select the science target and 2 guide stars and note down their approximate stellar centroids and edit planet.info and put those centroids into the planet.info using the example of stars already in the list. You need the channel number, star name, centroids, name of fits files, name of uncertainty files and prefix for the directory where the output will be saved.

1. Run aperture photometry photom_array_xo2.pro

Now we come to the nitty-gritty. Run the reduce routine from within photom_array_xo2.pro with the following commands photom_array_xo2,channel,radius,scale,star e.g.

photom_array_xo2,4,4.,1.,’wasp18′ ;Jan 2010

Most likely it will crash as the centroiding sub-routines failed to find the flux centroid in the pixels you stated in planet.info. Tweak around with the centroids in plane.info until there are no more crashes. You will get three HUGE files for the target star e..g

wasp18_ch4_flux_subsky_nrs_cntrd.txt
wasp18_ch4_flux_subsky_nrs_flratio.txt
wasp18_ch4_flux_subsky_nrs_px.txt
wasp18_ch4_flux_subsky_nrs.txt

which contain all the raw aperture photometry to be processed in the following step. Now I do know they could have been better handled as fits files, but what can you do. It’s now written this way.

1. Run overview program photom_loop.pro

Now we need to generate previews of the raw photometry and prepare input files for the Monte Carlo Markov chain, which removes the systematic effects while at the same time fits the secondary eclipse. Open the photom_loop.pro routines and use the following command to run the routine xo3_allrad,planet,path,ephemeris,rejt e.g.

xo3_allrad,’wasp17′,’/home/ivanmladek/XO/harrington/’,[55084.792935d,0.94145182d],0. ;from apj_709_1_159

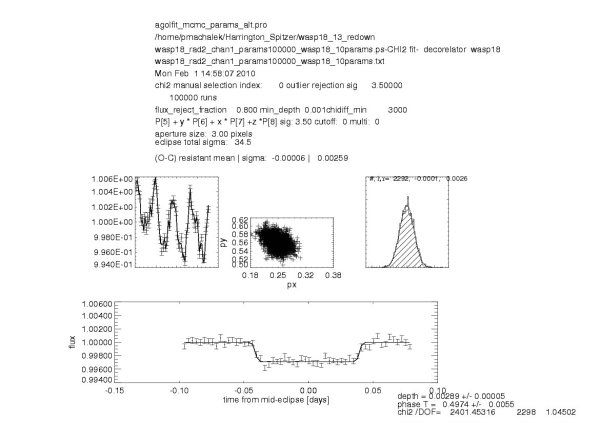
with the published ephemeris from the discovery or followup papers and 0. for the rejt, which is the number of minutes to reject from the beginning of the photometry. Repeat for all the channels you have. You should get images like this for each channel and for each photometry radius:

Left column is your target star and the middle and right columns are guide stars that you selected. The top row is the raw photometry for the given radius. The second row is the x and y centroids measure by flux weighted position (see Machalek et al. 2010 paper above for explanation). The third row is the background flux, then the first attempt at removing the systematic effect and the bottom row is the binned light curve after systematics removal. If this routine does not run properly or you can’t see the photometric points, just change the xrange for the phase displayed in photom_loop.pro . Make sure that the distributions for the x and y-centroids are not cut in half due to improper rounding up or rounding down and change accordingly in photom_loop.pro

1. Perform Monte Carlo Markov Chain (MCMC) determination of secondary eclipse parameters with proc2.pro

Now your working directory will contain a plethora of txt files of the form wasp18_model_rad5_chan4nrs0.589.txtcntrd with the collowing format

HJD, normalized stellar flux, un-normalized stellar flux, x-centroid, y-centroid, normalized stellar flux uncertainty, filename. Check whether the files actually contain number and not ****** symbols, which would mean that photom_loop.pro and it associated subroutines did not run properly. Usually either the flux or centroids don’t compile properly. Peek around in photom_loop.pro and plotnorm.pro to see what’s happening.

2454824.388059400022  1.0146714     2.32789E+05  0.3857398  0.6353102  0.0024323 SPITZER_I4_28775424_0029_0000_2_bcd.fits
2454824.388216900174  1.0021920     2.32789E+05  0.3839202  0.6107798  0.0049251 SPITZER_I4_28775424_0030_0000_2_bcd.fits
2454824.388369599823  1.0119270     2.32789E+05  0.3773899  0.6544900  0.0024167 SPITZER_I4_28775424_0031_0000_2_bcd.fits
2454824.388522299938  1.0120410     2.32789E+05  0.3769598  0.6296000  0.0024260 SPITZER_I4_28775424_0032_0000_2_bcd.fits
2454824.388679699972  1.0125369     2.32789E+05  0.3440900  0.6335101  0.0024339 SPITZER_I4_28775424_0033_0000_2_bcd.fits
2454824.388832500204  1.0117500     2.32789E+05  0.3566499  0.6351500  0.0023835 SPITZER_I4_28775424_0034_0000_2_bcd.fits
2454824.388989999890  1.0155903     2.32789E+05  0.3897200  0.6525502  0.0023921 SPITZER_I4_28775424_0035_0000_2_bcd.fits
2454824.389142700005  1.0104091     2.32789E+05  0.1992202  0.5787201  0.0024816 SPITZER_I4_28775424_0036_0000_2_bcd.fits
2454824.389300100040  1.0092218     2.32789E+05  0.3616900  0.6248202  0.0024621 SPITZER_I4_28775424_0037_0000_2_bcd.fits
2454824.389457600191  1.0114029     2.32789E+05  0.3613901  0.6031299  0.0023794 SPITZER_I4_28775424_0038_0000_2_bcd.fits

Now that we made sure that we have some flux files to feed to the Monte Carlo Markov Chain routine, a couple of caveats and explanations are in order. We will be removing systematics effects and fitting eclipse depths and eclipse centroids at the same time. Furthermore the systematics effects are different in channels 1, 2 and channels 3,4 (again see papers above). Hence the routine proc1.pro needs to be told, which channel we are using and then it takes off on the markov chain of usually 100,000 iterations, which takes a couple of hours on a typical 2GHz desktop with 1-2 GB of RAM for each channel per each photometric aperture radius. First we need to change proc1.pro to for the current star:

‘wasp18’:BEGIN
ephemeris=[0.94145182d,55084.792935d]
start=[[double((0.0206)/(1.216*0.004649)),double(cos(86.0/(180./!DPI))),0.05d,double(ephemeris[0]),double(ephemeris[1]),replicate(-10.^(-3.),5)] ]
;http://www.nature.com/nature/journal/v460/n7259/fig_tab/nature08245_T1.html
duration=0.08932*24.d ;http://www.nature.com/nature/journal/v460/n7259/fig_tab/nature08245_T1.html
END

where start is of the form start=[a_planet/r_star; cos(inclination); SQRT(eclipse depth estimate); period; ephemeris; MCMC jump probability parameters] .  The duration of the secondary eclipse also needs to be provided from the discovery paper. The MCMC routine is a tricky beast to run because we need to make sure that:

• First that the function defined for the removal of the systematics (transit or channel34_one which are defined at the top of proc1.pro) actually remove the systematics as they should. We can change the number of parameters and use quadratic terms for the subpixel x and y phase in transit or add quadratic ln(time) terms in channel34_one and we completely change the nature of the MCMC run. Most likely initially the MCMC run won’t even converge. A lot of patience and determination is needed here. Make sure when you change the systematic effect removal routines that on LINE 277 and LINE 377 of proc1.pro, you correctly check how many parameters need to be fitted for. Furthermore ensure that LINE713 & LINE729 show the correct parameter to perturb, otherwise your whole MCMC run will go wrong.
• Second once the MCMC is running, each parameter needs to make a jump in 20-40% of cases which is controlled by the MCMC jump probability parameters defined in the start variable in the header of proc1.pro. As the MCMC is running LINE805 is trying to automatically adjust the jump probability parameter so that you indeed get a 20-40% jump probability.
• For the first 2000 iterations you will get a visual overview how well your fit is going. If you are running proc1.pro on a cluster with no x.server, turn LINE790 & LINE 797 off.

So ready? Let’s start the MCMC run in the following format:  proc1,np,multi,sig,radius,phase,cutoff,channel,star; where np is the number of trials usually 100,000; multi is the 10^(index) for the MCMC jump probability variables, sig, is the number of sigmas at which at each step residuals will be removed to prevent a single high sigma outlier from skewing our results; radius is the radius aperture we are testing; phase is the string with which the photometry input *model*.txt files are labeled (do an ls in unix and see the txt file names); cutoff is the number of minutes that will not be used for fitting at the beginning of the photometry and finally star is the string label for the object that needs to match the photometry input txt file name.  Let’s try WASP-18 as an example:

proc1,100000,1E-3,3.5,4,0.396,0.,’4′,’wasp18′ ;Jan 2010

Now watch as the routine tries to fit the data over and over. Most likely it will crash. Try changing the starting parameter, the MCMC jump ratios, change the number of decorelation parameters, add or remove decorelations parameters. Once MCMC is purring along at 20-40% jump acceptance rate for EACH parameter, you should be good. It does not mean, though that this is the best MCMC run you could do, additional or fewer parameters could also help.  A nice MCMC output looks like:

———
1100.00       59.232568       5384.7787      1.10000
—–ij/ijt—–
0.30978261      0.19021739      0.19125683      0.23497268      0.25683060
0.36065574
—–bestfit—–
3.6439645     0.069756474     0.053368450      0.94145182      0.14687803
0.99187769      0.11293815     -0.22104302    0.0015535511   -0.0010000000
2071.4080       2188.0000
2071.4080
—–multinoise—–
100.231      10023.1      10.0231      100.231      100.231      1.00231
written filename: wasp18_rad1_chan1_params100000_wasp18_10params.fits
———
1200.00       64.182589       5348.5493      1.20000
—–ij/ijt—–
0.30000000      0.17500000      0.20500000      0.22500000      0.24500000
0.36500000
—–bestfit—–
3.6439645     0.069756474     0.054861034      0.94145182      0.14671054
0.99298630      0.11239299     -0.22321592    0.0012246178   -0.0010000000
2042.0034       2194.0000
2042.0034
—–multinoise—–
100.231      1002.31      10.0231      100.231      100.231      1.00231
written filename: wasp18_rad1_chan1_params100000_wasp18_10params.fits
———

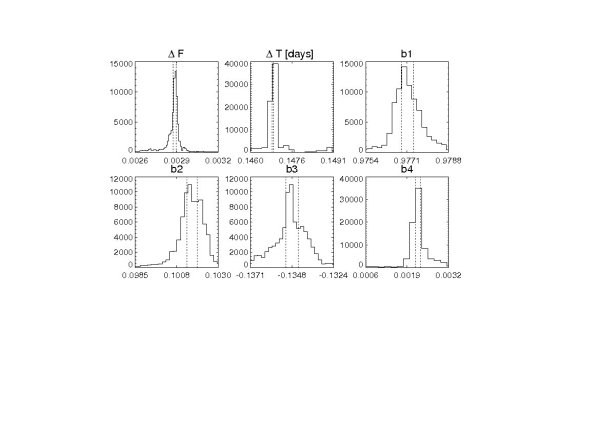
The output tells us that for 1100th iteration of the MCMC chain, 59 seconds have elapsed and hence around 5300 seconds total for the whole run are expected. The ij/ijt are the jump ratios for each parameter that should be between 20-40%. The first line of the bestfit parameters shows the eclipse paramaters: a(p)/r(star); cos(inclination); sqrt(eclipse depth); period; ephemeris. The second line of the bestfit shows the two to five systematic effect decorelation parameters depending on channel and how you defined them in proc1.pro in subroutines transit and channel34_one. The third bestfit line is the chi^2 and the degrees of freedom, which does change as at each step high-sigma outliers are rejected. Multinoise lists the MCMC jump probability variable which is adjusted during the first 2000 runs and finally the last line lists the fits file intow which the results are written every 100th iteration.

1. Analyze results of the MCMC fitting with agolfit_mcmc_params_alt.pro

Now we need to look at the results of the MCMC runs and check whether the chains have converged and what the resultant light curves look like. Run the allchannel_partial,channel,cutoff,label,nparam,directory,star routine from the agolfit_mcmc_params_alt.pro, where channel is the channel label, cutoff is the label for the phase of photometry file names, label is the string to describe the way we have decorelated the systematic effetcs, nparam is an obsoleted parameter that no longer does anything, directory is the directory with the fits files and star is the label for the star used in the fits file names e.g.

allchannel_partial,’4′,0.396,’P[7] * (alog(x))^(2.) + P[6] * alog(x) + P[5]’,7,’/home/pmachalek/Harrington_Spitzer/wasp18_24_redown’,’wasp18′

If executed properly, it will result in five postscript for each channel and each photometry radius:

wasp18_rad2_chan1_params100000_wasp18_10params_2.ps        ;overview of the finalized light curve

wasp18_rad2_chan1_params100000_wasp18_10params_chain.ps  ;overview of the steps of the MCMC chain
wasp18_rad2_chan1_params100000_wasp18_10params_corel.ps   ;overview of corelations between all the parameters
wasp18_rad2_chan1_params100000_wasp18_10params.ps            ; aposteriori distribution marginalized over each parameter

wasp18_rad2_chan1_params100000_wasp18_10params_unbinned.ps ; unbinned resultant light series

Furthermore ECL files are produced as well, which contain the details about the fitted eclipses, in a latex friendly format:

wasp18_rad2_chan1_params100000_wasp18_10params_baseline.ecl

wasp18_rad2_chan1_params100000_wasp18_10params.ecl contains latex formatted output for article writing.
\newcommand{\hotjupflone}{0.00289} %secondary eclipse depth
\newcommand{\hotjupeflone}{0.00005} %secondary eclipse depth uncertainty
\newcommand{\hotjuphjdone}{2504820.71329} %mid-centroid timing HJD
\newcommand{\hotjupehjdone}{0.00522} %mid-centroid timing HJD uncertainty
\newcommand{\hotjupdtone}{-3.5} % time offset in minutes from predicted mi-eclipse phase=0.5
\newcommand{\hotjupedtone}{7.5} % time offset in minutes from predicted mi-eclipse phase=0.5
\newcommand{\hotjupchione}{2.40145E+03} % time offset in minutes uncertainty from predicted mi-eclipse phase=0.5
\newcommand{\hotjupphaseone}{0.4974} %mid-centroid timing [phase]
\newcommand{\hotjupphaseone}{0.0055} %mid-centroid timing phase uncertainty
\newcommand{\hotjupgradone}{} %if linear gradient was used during MCMC in proc1.pro then for channel 1 and channel 2 decorelation this will be the slope
\newcommand{\hotjupegradone}{} if linear gradient was used during MCMC in proc1.pro then for channel 1 and channel 2 decorelation this will be the slope uncertainty

wasp18_rad2_chan1_params100000_wasp18_10params_flux.ecl
wasp18_rad2_chan1_params100000_wasp18_10params_phase_baseline.ecl
wasp18_rad2_chan1_params100000_wasp18_10params_phase_flux.ecl

When you are done inspecting the ecl files, copy the chosen aperture radius for each channel into a separate directory for final results plotting. 

1. Produce publishable figures and write paper

Use the plot_final.pro to plot the four channels of time series first uncorrected for the systematics and then corrected for the systematis:

plot_final,’baseline’,’xo3′ ; for the light curves with systematics left in

plot_final,’final’,’xo3′ ; for the de-correlated light curves.And now you have everything you need to write a paper: formatted results and publishable figures. All you need is the thinking. Good luck.

‘wasp18′:BEGIN        ;gaspar bakos light curve
dir=’/media/disk-1/backup/XO/harrington_cold_spitzer/_analyze/r28775424/ch2/bcd/’
cntroids=[[24.,26.],[61.,72.],[60.,51.],[61.,72.]]
cd,dir
list = file_search(‘*bcd.fits’)
elist = file_search(‘*bunc.fits’)
box_diameter=10.
print, cntroids   ;save_prefix=dir
save_prefix=’/media/disk-1/backup/XO/harrington_cold_spitzer/_analyze/r28775424/’
END